7/26/2019 Persamaan Pembentuk Aliran Governing Equ

1/19

Persamaan Pembentuk Aliran

(Governing Equations)

Persamaan pembentuk aliran yang mendasar untuk aliran fluida dan perpindahan

panas adalah dikembangkan dari tiga hukum kekekalan dalam fisika. Hukum kekekalan

tersebut adalah, kekekalan massa, kekekalan momentum, dan kekekalan energi. Hukum-

hukum kekekalan ini akan dibahas dalam bidang koordinat Kartesius.

2.1.1 Hukum Kekekalan Massa

Dengan menganggap sebuah elemen kecil dari fluida dalam bidang dua dimensi

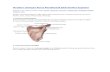
dengan dimensi xdan y seperti yang ditunjukkan oleh gambar 2.1. Konsep utama dalam

hal ini adalah bahwa kenaikan laju aliran massa pada volume kontrol adalah sama dengan

laju aliran massa netto yang melewati pada bagian saluran masuk dan saluran keluar.

dalam hal ini M adalah massa yang tersimpan didalam elemen fluida dan adalah laju

aliran massa yang melewati permukaan dari elemen tersebut.

Gambar 2.1 Sebuah elemen fluida untuk hukum kekekalan massa dalam dua dimensi

Dengan menggunakan simbol-simbol pada gambar diatas, persamaan dapat diperluas

menjadi

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

2/19

Dengan menyelesaikan persamaan ini dan membaginya dengan ukuran elemen xy,

sehingga

Untuk mengembangkan persamaan yang sama untuk aliran tiga dimensi, elemen

yang sama dari fluida seperti yang ditunjukkan oleh gambar 2.2. Pada gambar komponen

kecepatan pada sumbu-z disebut w. Dengan menggunakan konsep seperti yang

digambarkan pada gambar, persamaan (2.1) memberikan

Dengan menyelesaikan persamaan ini dan membaginya dengan ukuran elemen xy z

yaitu

Dengan menggunakan operator divergensi, persamaan (2.5) dapat dituliskan sebagai berikut

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

3/19

Gambar 2.2 Sebuah elemen fluida untuk hukum kekekalan massa dalam tiga dimensi

Persamaan hukum kekekalan massa seperti yang ditunjukkan oleh persamaan (2.5)

dapat dituliskan sebagai berikut

Dengan menggunakan persamaan berikut yang didefenisikan sebagai

Dan dengan menggunakan operator divergensi,

Persamaan (2.7) dapat dituliskan menjadi bentuk yang sederhana yakni sebagai berikut

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

4/19

Persamaan diatas adalah bentuk umum dari hukum kekekalan massa atau juga dikenal

dengan persamaan kontinuitas. Dalam hal aliran inkompresibel, yang berarti bahwa variasi

temporal dan spasial dalam rapat massa adalah diabaikan, persamaan ini dapat

disederhanakan dengan menghilangkan D/Dtdari persamaan. Sehingga, persamaan

kontinuitas dapat dituliskan sebagai berikut ini

denganxi, i= 1,2,3 menunjuk pada sumbux,y,z

2.1.2 Hukum Kekekalan Momentum

Hukum ini juga dikenal sebagai hukum kedua Newton. Hukum tersebut

mengatakan bahwa gaya resultan yang bereaksi pada objek sama dengan percepatan

dikalikan dengan massa objek tersebut. Sebuah elemen fluida kecil dalam bidang dua

dimensi dengan dimensi xdanyseperti yang ditunjukkan oleh gambar 2.3. Pada bidang

dua dimensi, gaya hanya berada pada sumbu-x dan sumbuy. Pada gambar tersebut, hanya

gaya pada sumbu-x yang ditampilkan. Gaya bereaksi pada elemen yakni gaya padapermukaan dan gaya pada body elemen. Gaya pada permukaan diakibatkan oleh distribusi

tekanan, tegangan normal, dan tegangan geser.Gaya pada body dinotasikan sebagaif, yang

didefenisiskan sebagai gaya per unit massa yang bereaksi pada pusat dari elemen fluida.

Pada keadaan yang sebenarnya gaya ini dapat berupa gaya gravitasi, listrik, dan gaya

magnet.

Gambar 2.3 Sebuah elemen fluida untuk hukum kekekalan momentum dalam dua dimensi

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

5/19

Hukum kedua Newton pada arahx dapat dituliskan sebagai berikut

Fx= max

, Fx dan ax adalah gaya-gaya resultan dan percepatan pada arah-x. Dengan mensubstitusi

semua gaya-gaya yang berada di gambar dan dengan menggunakan defenisi daripercepatan ax =Du/Dt, persamaan (2.11) dapat dijabarkan sebagai berikut

Dengan menyelesaikan persamaan ini dan mensubstitusi massa m=xy sehingga

Dengan membagi persamaan diatas dengan xy, kita mendapatkan persamaan seperti

yang ada dibawah ini :

Untuk menghasilkan persamaan momentum yang lebih lengkap dari sebuah elemen

fluida maka dapat dilakukan pada bidang tiga dimensi seperti yang ditunjukkan oleh gambar

2.4. Pada gambar hanya gaya-gaya pada arah-x yang ditunjukkan. Sebagai catatan bahwadalam tiga dimensi, ada enam gaya normal dan gaya geser yang bekerja pada permukaan

elemen. Gaya-gaya ini, dua buah gaya berasal dari distribusi tekanan dan gaya yang berasal

dari dalam elemen fluida tersebut seperti yang tergambar pada gambar tersebut.

Dengan mensubstitusi gaya-gaya ini kedalam defenisi dari hukum kedua Newton

pada persamaan (2.11) yaitu

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

6/19

Dengan menyelesaikan persamaan ini dan membaginya dengan xyz,diperoleh hasil yang

lebih lengkap sebagai berikut :

Gambar 2.4 Sebuah elemen fluida untuk hukum kekekalan momentum dalam tiga dimensi

Dengan menggunakan cara yang sama, persamaan

dan,

Persamaan diatas diperoleh dari elemen fluida yang bergerak dengan aliran atau dikenal

sebagai bentuk yang tidak kekekalan momentum. Persamaan diatas dibentuk dari turunan

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

7/19

yang harus dikonversikan kedalam bentuk persamaan yang kekekalan momentum. Untuk

lebih mudahnya, proses pengkonversian Du/Dt yang ditunjukkan oleh berikut ini.

Dengan mengembangkan persamaan turunan tersebut dan menggunakan identitasdivergensi dari sebuah produk skalar yakni

dan

Dengan mensubstitusi persamaan (2.19) dan persamaan (2.20) kedalam persamaan (2.18)

menghasilkan

yang kemudian dapat disusun menjadi persaman berikut

Istilah lain dari persamaan ini adalah sama dengan nol seperti yang ditujukkan oleh

persamaan (2.6). Sehingga persamaan (2.22) dapat dituliskan sebagai berikut

Dengan mensubstitusi persamaan (2.23) kedalam persamaan (2.17) menghasilkan bentuk

persamaan kekekalan momentum searah sumbu-x

Dengan cara yang sama, persamaan dalam arah sumbu-y dan sumbu-z yaitu

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

8/19

Persamaan (2.24) juga dikenal sebagai persamaan Navier-Stokes dalam bentuk konservasi.

Jika kurva tingkat fluida stress versus strain diplot, ada dua fenomena yang dapat

ditarik(diketahui). Ada fluida dengan kurva linear dan satunya lagi dengan kuva non linear.

Fluida dengan kurva linear dikenal dengan fluida Newtonian, sebagai contoh air. Fluida

dengan kurva non linear di kenal dengan fluida non- Newtonian,sebagai contoh

darah.Dalam disertasi ini kita hanya mempertimbangkan fluida Newtonian. Untuk fluida ini,

tegangan normal dapat dirumuskan sebagai berikut.

Dan tegangan geser

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

9/19

Dimana adalah gradien kurva laju stress versus strain atau dikenal dengan viskositas

molekul (sangat dikenal dengan viskositas dinamis) dan adalah viskositas kedua. Kedua

viskositas ini berkaitan dengan viskositas bulk (k) dengan persamaan k=2

3+ (2.27)

Secara umum , diyakini bahwa viskositas bulk diabaikan kecuali dalam studi struktur

gelombang kejut dan penyerapan dan redaman dari gelombang akustik. Dengan kata lain,

untuk hampir semua fluida viskositas bulk sama dengan nol atau k= 0 . Jadi viskositas kedua

menjadi =2

3(2.28).

Sebagai catatan hipotesis ini diperkenalkan oleh Stokes pada tahun 1845. Meskipun

hipotesis masih belum pasti dikonfirmasi,bagaimanapun, sering digunakan untuk saat ini.

Karya ini disertakan. Mengganti hipotesis dan persamaan tegangan normal dan geser ke

dalam persamaan (2.24) kita memperoleh persamaan lengkap Navier-Stokes.

Persamaan ini dapat ditulis dengan lebih lengkap dengan menggunakan persamaan tensor.

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

10/19

Dimana i,j,k = 1,2,3 menunjukkan x,y,z, masing-masing sumbu.

2.1.3 The Law conservation of energy ( Konservasi Hukum Energi)

Pada bagian ini, prinsip fisik ketiga yaitu energi yang di konservasi diterapkan.

Menyatakan perubahan tingkat energi di dalam (E) sebuah elemen adalah sama dengan

jumlah dari fluks panas bersih (Q) kedalam elemen dan tingkat kerja yang dilakukan Wpada

elemen oleh bodydan kekuatan permukaan. Hukum ini di tuliskan E= Q+ W (2.31)

Tingkat pekerjaan yang dilakukan pada elemen oleh body dan kekuatan permukaan akan

dievaluasi pertama. Perhatikan elemen kecil dari fluida seperti ditunjukkan pada Gambar

2.5. Perhatikan di sini ada gaya akibat daerah tekan karena tekanan normal dan geser dan

karena gaya body. Sebagai catatan definisi tingkat kerja yang dilakukan pada elemen adalah

gaya dikalikan dengan kecepatan. Dengan demikian semua gaya di tunjukkan di sini. Namun

akan sangat jelas jika semua gaya di gambarkan pada elemen yang sama. Untuk

membuatnya sederhana, hanya gaya di sumbu x yang di tunjukkan pada gambar. Gaya-gaya

ini akan di evaluasi terlebih dahulu dan cara yang sama akan digunakan untuk mengevaluasi

kerja oleh gaya pada sumbu y dan sumbu z.

Gambar 2.5 Kerja yang dilakukan di elemen oleh gaya pada sumbu x

7/26/2019 Persamaan Pembentuk Aliran Governing Equ

11/19

Dengan menggunakan definisi, tingkat kerja o